Pedro Henrique Muniz de Oliveira
Turma 2001 Integral
O que é um cone?
O cone é um importante sólido geométrico, que é estudado na geometria espacial. Ele é classificado como um corpo redondo ou sólido de revolução por ter um círculo como base e por ser construído a partir da rotação de um triângulo. Ele pode ser classificado como um cone oblíquo ou cone reto, e este poder ser equilátero ou não. Em todos os sólidos geométricos, vale ressaltar a importância do cálculo da área total, ou seja, a soma da área das figuras que fazem parte do sólido que o compõem, e de seu volume, que é o espaço ocupado pelo corpo. Vale ressaltar que, no cone, existem formas específicas para o cálculo da área total e do volume, as quais serão apresentadas no decorrer deste texto.

Elementos de um cone
Bastante presente no nosso cotidiano e considerado um importantíssimo sólido geométrico, o cone é conhecido como um dos corpos redondos ou sólidos de revolução pela característica que ele possui de ter uma base circular e por ser construído a partir da rotação de um triângulo, conhecida também como revolução de um triângulo .
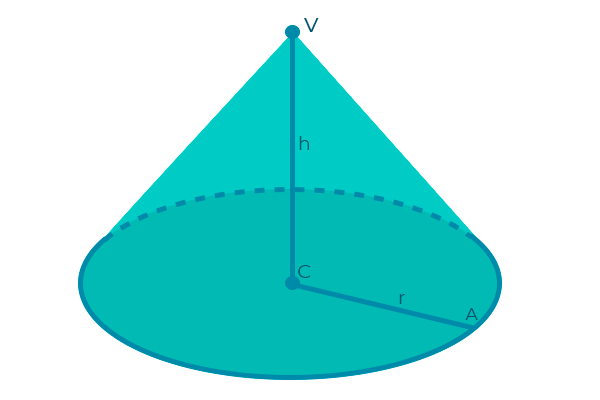
Por ter uma base circular (C), na geometria plana, devemos considerar o seu raio (r), que é um elemento importantíssimo para os cálculos e estudos do cone. Além do raio da base, a altura (h) também é um elemento importante, pois ela liga o vértice (V) à base de forma perpendicular.
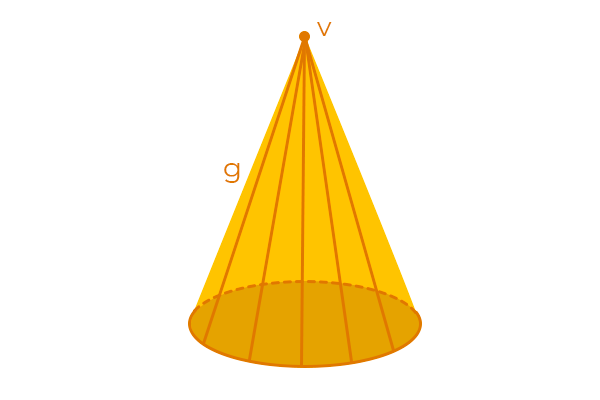
Outro elemento bastante importante no cone são as suas geratrizes (g), que são semirretas que ligam o vértice às extremidades da circunferência. Elas são infinitas. Veja algumas delas:
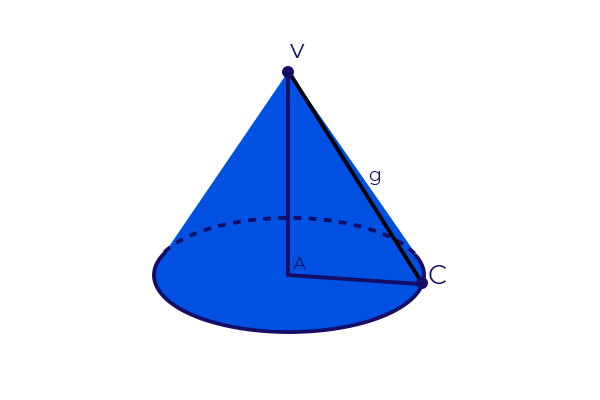
Para calcular a geratriz de um cone reto, usamos o teorema de Pitágoras, a partir da altura (h), raio (r) e geratriz (g)
Analizando o triângulo pelo teorema de Pitágoras, podemos afirmar que g é a hipotenusa do triângulo, h e r são os catetos desse triângulo, logo, temos que:
g2=h2+r2
Área do cone
Para calcular a área total de qualquer sólido geométrico, devemos calcular a área das figuras planas que formam o sólido, logo é importante conhecer a planificação do cone.
Podemos ver que a área da base (Ab) é a área de um círculo de raio r e que a área lateral (Al) é a área de um arco. Vamos calcular cada uma delas separadamente para chegarmos à área total.
=Al+Ab
Área da base: como a base é um círculo, então é igual a πr²:
= πr²
Área lateral: a área de um setor circular, que é dada por:
= π . r . g
Conhecendo as fórmulas da área lateral e da área da base, podemos reescrever a área total do cone, que pode ser calculada por:
At= πr (r + g)
Volume do cone
Cálculo de grande importância, assim como a área total, o volume do cone é calculado a partir de uma fórmula que leva em consideração a área da base e a altura do cone. Vale ressaltar que cones com mesma altura e mesmo raio possuem a mesma área, ou seja, se houver um cone reto de altura h e raio r e um cone oblíquo com mesma altura e raio, o volume deles será o mesmo. O volume é dado pela multiplicação da área da base (como a base é um círculo: ) e a altura dividida por três.